Neural Fields as Distributions:
Signal Processing Beyond Euclidean Space

Neural fields have emerged as a powerful and broadly applicable method for representing signals. However, in contrast to classical discrete digital signal processing, the portfolio of tools to process such representations is still severely limited and restricted to Euclidean domains.

In this paper, we address this problem by showing how a probabilistic re-interpretation of neural fields can enable their training and inference processes to become "filter-aware". The formulation we propose not only merges training and filtering in an efficient way, but also generalizes beyond the familiar Euclidean coordinate spaces to the more general set of smooth manifolds and convolutions induced by the actions of Lie groups. We demonstrate how this framework can enable novel integrations of signal processing techniques for neural field applications on both Euclidean domains, such as images and audio, as well as non-Euclidean domains, such as rotations and rays. A noteworthy benefit of our method is its applicability. Our method can be summarized as primarily a modification of the loss function, and in most cases does not require changes to the network architecture or the inference process.

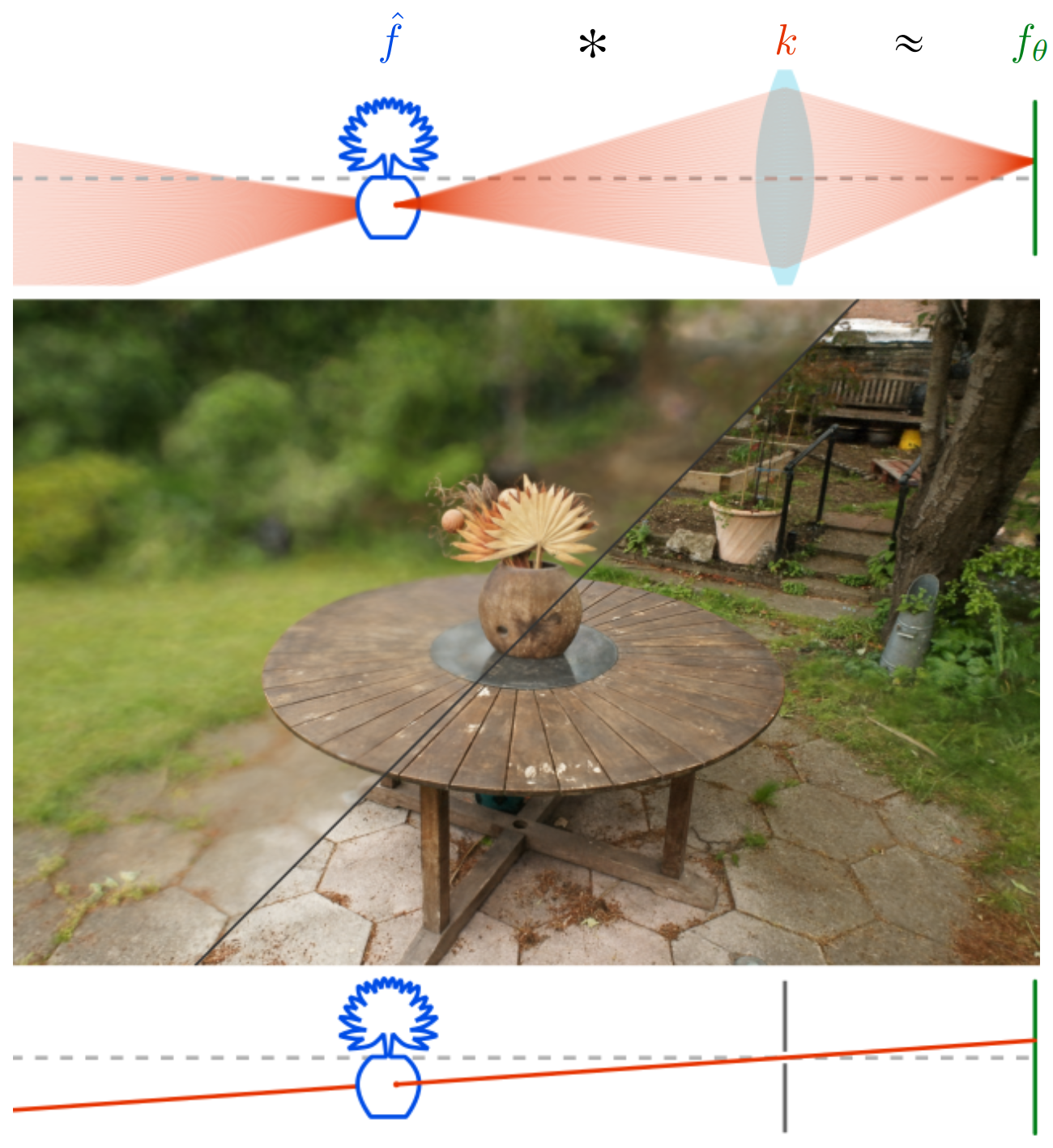
Our method enables a variety of neural field-based methods to be reinterpreted within a common framework of non-Euclidean signal processing. For example, we show how the simulation of lens effects, such as depth of field (top), can be implemented without extra inference cost as a linear filter applied at training time. This filtering operation is realized as a group convolution via the action of SE(3) between the light field of the scene ƒ̇̂ and distribution of rays, k. Our training process results in the observed light field being directly approximated by the learned network ƒ_𝜃 ≈ ƒ̇̂ ✻ k. In the case where a typical pinhole camera model is desired, our method reduces to convolving with a Dirac delta distribution over the ray manifold (bottom).